Welcome to your journey into Calculus 1! This guide simplifies complex concepts, making them accessible to everyone․ Discover the fundamentals, importance, and practical applications of calculus․

1․1 What is Calculus and Why is it Important?

Calculus is a branch of mathematics that studies change and motion․ It involves limits, derivatives, and integrals, which help describe how things change over time or space․ Unlike algebra or geometry, calculus focuses on rates of change and accumulation, making it essential for modeling real-world phenomena․ Its applications span science, engineering, economics, and more, providing tools to solve complex problems․ Understanding calculus is crucial for advancing in STEM fields and developing problem-solving skills, making it a cornerstone of modern mathematics․

1․2 Understanding the Basics of Calculus 1

Calculus 1 introduces foundational concepts like functions, limits, and derivatives․ It explores how functions behave, preparing you for more complex topics․ Start by mastering basic algebra and geometry, as these are essential for understanding limits and derivatives․ Calculus 1 focuses on differentiation, which measures rates of change․ Grasp these fundamentals to build a strong foundation for advanced calculus․ Regular practice and conceptual clarity will help you excel in problem-solving․

Setting Up Your Learning Environment

Create a quiet, organized workspace with essential tools like graph paper, a scientific calculator, and access to textbooks or online resources for easy reference․

2․1 Choosing the Right Study Materials

Selecting the right study materials is crucial for mastering Calculus 1․ Opt for a clear, beginner-friendly textbook that explains concepts in simple terms․ Supplementary resources like workbooks or online guides can provide additional practice problems․ Ensure your materials include step-by-step examples and visual aids to help you grasp complex ideas․ Prioritize resources with a focus on foundational understanding rather than overly advanced content․ This will help you build a solid base for more challenging topics ahead․

2․2 Tools and Resources for Learning Calculus

To excel in Calculus 1, utilize essential tools and resources․ Graphing calculators like TI-84 or Desmos help visualize functions and derivatives․ Online platforms such as Khan Academy, MIT OpenCourseWare, and Wolfram Alpha provide free tutorials and problem-solving aids․ Video tutorials on YouTube offer diverse teaching styles, while mobile apps like Photomath and Symbolab assist with step-by-step solutions․ Join Reddit forums (e․g․, r/learnmath, r/calculus) for community support, and explore textbooks like Calculus for Dummies or Stewart’s Calculus for comprehensive guidance․

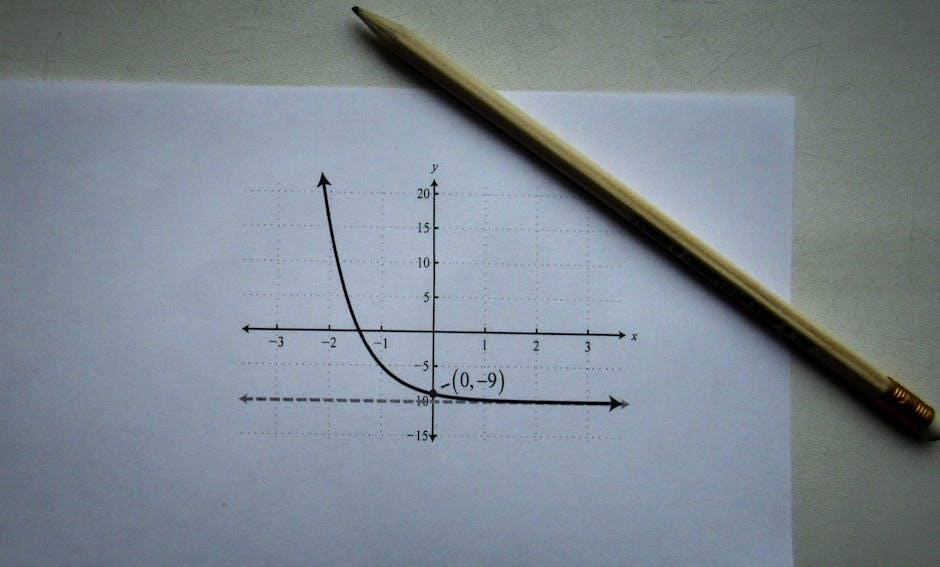
Basic Concepts in Calculus 1

Calculus 1 begins with core principles like functions, graphs, and foundational concepts․ Understanding these basics is essential for mastering limits, derivatives, and integrals․
Understanding functions is essential in calculus․ A function relates inputs (domain) to outputs (range), and graphs provide visual representations․ Key concepts include linear, quadratic, and polynomial functions․ Graphing helps identify patterns, trends, and behavior, such as increasing/decreasing intervals and intercepts․ Functions form the foundation for limits, derivatives, and integrals․ Grasping function properties and their graphical interpretations is critical for problem-solving in calculus․ Start by analyzing simple functions to build intuition and familiarity with their behavior․

3․2 Understanding Limits and Continuity

Understanding limits and continuity is crucial in Calculus 1․ Limits determine the behavior of functions as they approach specific points, while continuity ensures no abrupt jumps or breaks․ Mastering these concepts helps in analyzing function behavior, essential for derivatives and integrals․ Limits are evaluated using algebraic manipulation, numerical approaches, or graphical analysis․ Continuity is confirmed when a function’s limit at a point equals its function value there․ Grasping these ideas is vital for tackling more complex calculus topics and real-world applications․

The Fundamentals of Limits

Limits are the cornerstone of calculus, defining how functions behave as inputs approach specific values․ They help understand continuity and are essential for derivatives and integrals․

Grasping limits is crucial for solving problems involving change and accumulation․ They provide a mathematical way to handle infinity and instantaneous rates, fundamental in calculus․

4․1 Evaluating Limits: Step-by-Step Guide

Evaluating limits is a foundational skill in calculus․ Start by substituting the input value directly into the function․ If this results in an indeterminate form (like 0/0), simplify the expression by factoring or canceling terms․ For rational functions, try factoring numerator and denominator․ If substitution still doesn’t work, use conjugate multiplication or L’Hôpital’s Rule for 0/0 or ∞/∞ forms․ Always consider one-sided limits if a two-sided limit doesn’t exist․ Practice these methods to master limit evaluation․

4․2 Solving Limit Problems: Tips and Tricks

Mastering limit problems requires a strategic approach․ Start by understanding the intuitive concept of limits and practice substituting values directly․ Factor and cancel expressions to simplify indeterminate forms․ Use L’Hospital’s Rule for 0/0 or ∞/∞ scenarios․ Always check one-sided limits when evaluating two-sided limits․ Look for asymptotes and discontinuities to identify where limits may not exist․ Practice with graphical interpretations to visualize function behavior․ Regular practice builds intuition and problem-solving speed․

• Focus on simplifying expressions first․
• Leverage graphical tools for better understanding․
• Review algebraic manipulation techniques․

Derivatives: The Core of Calculus 1

Derivatives measure how functions change, central to Calculus 1․ They describe rates of change and slopes, essential for optimization and understanding dynamic systems in various fields like physics and economics․

5․1 What are Derivatives and Their Applications?

Derivatives measure how a function changes as its input changes, representing the instantaneous rate of change․ They are fundamental in calculus, describing slopes of tangent lines and velocity․ Derivatives are crucial in physics, engineering, and economics for modeling growth, optimization, and rates of change․ Understanding derivatives helps solve real-world problems, such as calculating acceleration or maximizing profit․ Their applications are vast, making them a cornerstone of calculus and essential for problem-solving in various fields․

5․2 Calculating Derivatives: Rules and Shortcuts

Mastering derivatives begins with essential rules․ The Power Rule simplifies differentiation of monomials, while the Product and Quotient Rules handle more complex functions․ Chain Rule is key for composites․ Shortcut tips include recognizing patterns, using derivatives of basic functions, and applying constant multiple rules․ Practice these techniques to build speed and accuracy․ Avoid common mistakes like misapplying rules or forgetting to apply the chain rule․ With consistent practice, calculating derivatives becomes second nature․

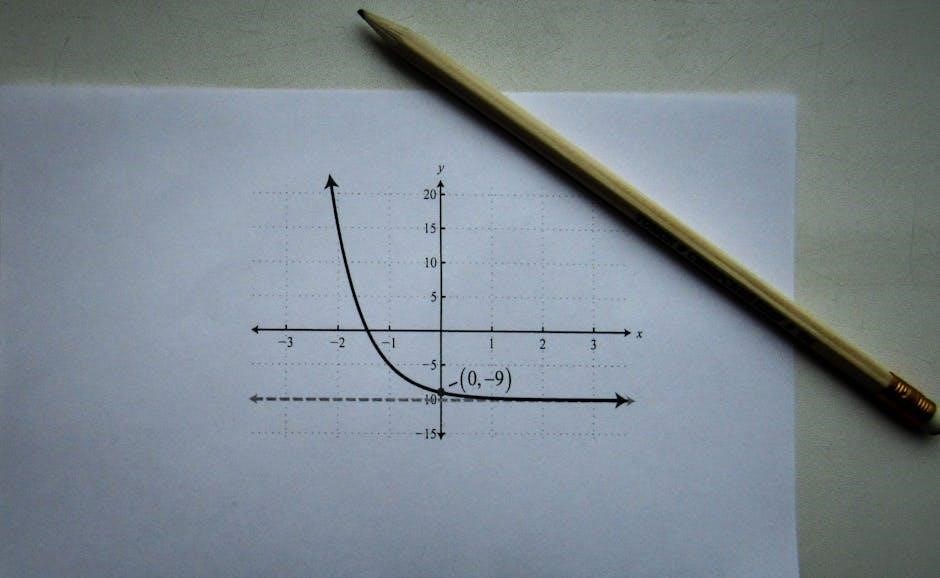
Integration: The Other Half of Calculus

Integration is the reverse process of differentiation, allowing us to find the area under curves and solve real-world problems in physics, engineering, and economics․

6․1 Understanding Integrals and Their Importance

Integrals are a fundamental concept in calculus, representing the accumulation of quantities over an interval․ They are used to calculate area under curves, volumes, and other physical measurements․ Unlike derivatives, which focus on rates of change, integrals emphasize the total quantity․ They are essential in physics, engineering, and economics for modeling real-world phenomena, such as motion and energy․ Mastering integrals is crucial for understanding calculus and its applications․

6․2 Basic Integration Techniques for Beginners

Mastering basic integration techniques is essential for solving calculus problems․ Start with simple methods like substitution and the power rule․ The substitution method simplifies complex integrals by changing variables․ The power rule integrates monomials easily․ Additionally, learn to integrate constants and apply the constant multiple rule․ Practice these techniques with sample problems to build confidence․ Remember, integration is the reverse process of differentiation, so understanding derivatives will help․ Keep practicing to grasp these fundamental skills․

Common Mistakes to Avoid in Calculus 1

Calculus newcomers often misapply limit rules or mishandle derivative calculations․ Forgetting continuity conditions and improper integral setups are also frequent pitfalls․ Stay vigilant and double-check your steps․

7․1 Pitfalls in Solving Limit and Derivative Problems

When solving limit problems, common mistakes include mishandling infinity, misapplying L’Hôpital’s Rule, and ignoring one-sided limits․ For derivatives, errors often arise from incorrect rule applications, such as misusing the product or quotient rule․ Many students also forget to simplify functions before taking limits or derivatives․ Additionally, neglecting to check for continuity or differentiability at points can lead to incorrect solutions․ Always double-check algebraic manipulations and apply rules carefully to avoid these pitfalls․

7․2 Avoiding Errors in Integration

Integration can be tricky, but avoiding common errors ensures accuracy․ Always double-check substitution steps, ensure proper sign handling, and verify the limits of integration․ Mistakes often arise from misapplying rules or forgetting constants․ Be cautious with negative signs and exponents, as they significantly impact results․ Regular practice and reviewing steps can minimize errors․ Using online tools to verify solutions helps build confidence and identifies overlooked mistakes․ Stay attentive to detail to master integration successfully․

Practicing with Sample Problems

Practicing with sample problems is essential for mastering Calculus 1․ It reinforces concepts, enhances problem-solving skills, and prepares you for exams․ Start with basic limits, derivatives, and integrals to build confidence and understanding․ Regular practice helps identify weak areas and improves overall performance․

8․1 Solving Limits and Derivatives: Practice Exercises

Mastering limits and derivatives requires consistent practice․ Start with basic limit problems, such as evaluating limits algebraically or using L’Hôpital’s Rule․ For derivatives, practice finding rates of change and slopes of tangent lines․ Use online platforms or textbooks for exercises․ Check solutions to understand mistakes․ Gradually move to more complex problems, like limits involving trigonometric functions or derivatives of composite functions․ Regular practice builds confidence and fluency in calculus fundamentals․

8․2 Integration Practice: Step-by-Step Solutions

Master integration with hands-on practice! This section provides detailed, step-by-step solutions to common integral problems․ Start with basic polynomials, then move to trigonometric functions, exponentials, and more complex forms․ Each problem is broken down to help you understand the process․ Learn how to apply substitution, integration by parts, and other essential techniques․ Examples include definite and indefinite integrals, with clear explanations of each step․ Practice regularly to build confidence and fluency in solving integrals․

Tips for Mastering Calculus 1

Mastering Calculus 1 requires consistent practice, understanding core concepts, and breaking problems into manageable steps․ Use visual aids and seek help when needed to build confidence and proficiency․

9․1 Building a Strong Foundation in Algebra and Geometry

A strong foundation in algebra and geometry is essential for mastering Calculus 1․ Algebra helps with solving equations, understanding functions, and manipulating expressions—critical skills for limits and derivatives․ Geometry provides spatial reasoning and insights into shapes, graphs, and coordinate systems․ Focus on understanding function properties like even and odd functions, as well as trigonometric identities․ Regular practice solving algebraic and geometric problems will build the confidence and skills needed for calculus success․ Start with basic concepts and gradually progress to more complex problems․

9․2 Time Management and Study Habits for Success

Effective time management and consistent study habits are crucial for mastering Calculus 1․ Set a regular study schedule, dedicating specific times to problem-solving and concept review․ Break study sessions into manageable chunks to maintain focus․ Prioritize challenging topics and tackle them early when your mind is fresh․ Use active learning techniques, such as solving problems and self-quizzing, to reinforce understanding․ Stay consistent, review notes daily, and use a planner to track progress․ Seek help when stuck, and celebrate small achievements to stay motivated․

Congratulations on completing Calculus 1 for Dummies! You’ve mastered limits, derivatives, and integrals, unlocking the door to understanding rates of change and accumulation․ Keep exploring and applying these concepts to real-world problems—your journey in calculus has just begun!

10;1 Recap of Key Concepts in Calculus 1

In this final recap, we revisit the cornerstone concepts of Calculus 1: limits, derivatives, and integrals․ Limits explore function behavior, derivatives measure rates of change, and integrals calculate accumulation․ These tools are fundamental for understanding optimization, motion, and area under curves․ Mastery of algebra and problem-solving skills is crucial․ By applying these principles, you can tackle real-world challenges with confidence․ Keep practicing, and remember, calculus is a powerful language for describing change and continuity in our universe․